Dynamic Programming
Repetitive subproblems => use Dynamic Programming.
Increases CPU efficiency.
2 techniques (either can be recursive or iterative)
Increases CPU efficiency.
2 techniques (either can be recursive or iterative)
- memoization: uses dictionary/hashmap, recursion, top-down (starts w/ the final condition and recursively gets result of sub-problems)
- tabulation: uses 2-D array, iterative, bottom-up (starts with base-condition until final result is reached)
Longest Common Subsequence
If S1 and S2 are the two given sequences then, Z is the common subsequence of S1 and S2 if Z is a subsequence of both S1 and S2. Furthermore, Z must be a strictly increasing sequence of the indices of both S1 and S2 but not necessairily contiguous.
Below is a naive implementation
def lcs(X, Y, m, n):
# Base case
if m == 0 or n == 0:
return 0
# if the last characters in both strings are the same, add 1 to the lcs of the remaining string
elif X[m-1] == Y[n-1]:
return 1 + lcs(X, Y, m-1, n-1)
else:
return max(lcs(X, Y, m, n-1), lcs(X, Y, m-1, n))
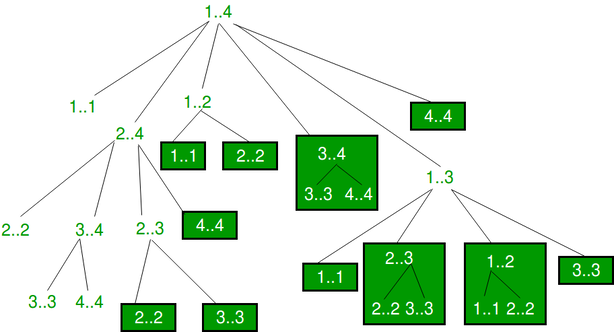
Time Complexity is O(2^n) but this can be improved through dynamic programming and memoization
If we take a look at the recursion tree
lcs("AXYT", "AYZX")
/ \
lcs("AXY", "AYZX") lcs("AXYT", "AYZ")
/ \ / \
lcs("AX", "AYZX") lcs("AXY", "AYZ") lcs("AXY", "AYZ") lcs("AXYT", "AY")
Since there are repetition, we can use a 2-D array to store previous sub-call results
Time Complexity: O(m * n)
If S1 and S2 are the two given sequences then, Z is the common subsequence of S1 and S2 if Z is a subsequence of both S1 and S2. Furthermore, Z must be a strictly increasing sequence of the indices of both S1 and S2 but not necessairily contiguous.
Below is a naive implementation
def lcs(X, Y, m, n):
# Base case
if m == 0 or n == 0:
return 0
# if the last characters in both strings are the same, add 1 to the lcs of the remaining string
elif X[m-1] == Y[n-1]:
return 1 + lcs(X, Y, m-1, n-1)
else:
return max(lcs(X, Y, m, n-1), lcs(X, Y, m-1, n))
Time Complexity is O(2^n) but this can be improved through dynamic programming and memoization
If we take a look at the recursion tree
lcs("AXYT", "AYZX")
/ \
lcs("AXY", "AYZX") lcs("AXYT", "AYZ")
/ \ / \
lcs("AX", "AYZX") lcs("AXY", "AYZ") lcs("AXY", "AYZ") lcs("AXYT", "AY")
Since there are repetition, we can use a 2-D array to store previous sub-call results
Time Complexity: O(m * n)
|
# Memoized
def lcs(X, Y, m, n, dp): if (m == 0 or n == 0): return 0 if (dp[m][n] != -1): return dp[m][n] if X[m - 1] == Y[n - 1]: dp[m][n] = 1 + lcs(X, Y, m - 1, n - 1, dp) return dp[m][n] dp[m][n] = max(lcs(X, Y, m, n - 1, dp),lcs(X, Y, m - 1, n, dp)) return dp[m][n] # Driver code X = "AGGTAB" Y = "GXTXAYB" m = len(X) n = len(Y) dp = [[-1 for i in range(n + 1)]for j in range(m + 1)] print(lcs(X, Y, m, n, dp)) |
# Tabulated
def lcs(X , Y): m = len(X) n = len(Y) # declaring the array for storing the dp values L = [[None]*(n+1) for i in range(m+1)] for i in range(m+1): for j in range(n+1): if i == 0 or j == 0 : L[i][j] = 0 elif X[i-1] == Y[j-1]: L[i][j] = L[i-1][j-1]+1 else: L[i][j] = max(L[i-1][j] , L[i][j-1]) return L[m][n] |
Subset Sum
Given a set of non-negative integers, and a value sum, determine if there is a subset of the given set with sum equal to given sum.
Naive solution = cycle through all subsets of n numbers and, check each subset => running time is of order O(n * (2^n))
Subset sum is a type of the 0–1 Knapsack problem.
Time Complexity: O(sum * n), Space Complexity: O(sum* n)
Given a set of non-negative integers, and a value sum, determine if there is a subset of the given set with sum equal to given sum.
Naive solution = cycle through all subsets of n numbers and, check each subset => running time is of order O(n * (2^n))
Subset sum is a type of the 0–1 Knapsack problem.
Time Complexity: O(sum * n), Space Complexity: O(sum* n)
|
def subsetSum(A, n, k, lookup):
# if k equals 0 then empty set is a subset of itself or through recursion, we have summed up to exactly k if k == 0: return True # base case: no items left, or sum becomes negative if n <= 0 or k < 0: return False # Construct a unique key key = (n, k) if key not in lookup: # Case 1. Include the current item include = subsetSum(A, n - 1, k - A[n], lookup) # Case 2. Exclude the current item exclude = subsetSum(A, n - 1, k, lookup) # Assign true if we get subset by including or excluding the current item lookup[key] = include or exclude return lookup[key] |
def isSubsetSum(set, n, sum):
# Initialize 2-D array subset = [[False] * (sum + 1) for i in range(n + 1)] # If sum is 0, then true for i in range(n + 1): subset[i][0] = True # If sum not 0 and empty set, then false for i in range(1, sum + 1): subset[0][i]= False # Fill the subset table in bottom up manner for i in range(1, n + 1): for j in range(1, sum + 1): # If the current number is greater than the target sum, skip it if j<set[i-1]: subset[i][j] = subset[i-1][j] else: # Check if either including the current number # or excluding it can achieve the target sum subset[i][j] = (subset[i-1][j] or subset[i - 1][j-set[i-1]]) return subset[n][sum] |
0/1 Knapsack Problem
* There are 2 types of knapsack problem: 0/1 => solved using dynamic programming, and fractional => solved using greedy algorithm
Given:
Find:
A brute force solution is to look through all subsets as shown below which has a time complexity of O(2^n)
* There are 2 types of knapsack problem: 0/1 => solved using dynamic programming, and fractional => solved using greedy algorithm
Given:
- Maximum weight M and the number of packages n.
- Array of weight W[i] and corresponding value V[i].
Find:
- Items that need to be put in the knapsack to maximize value and keep weight under M
A brute force solution is to look through all subsets as shown below which has a time complexity of O(2^n)
Time Complexity: O(capacity * n), Space Complexity: O(capacity * n)
def knapSack(C, wt, val, n):
K = [[0 for j in range(C + 1)] for i in range(n + 1)]
for i in range(n + 1):
for j in range(C + 1):
if i == 0 or j == 0:
K[i][j] = 0
if j < wt[i-1]:
K[i][j] = K[i-1][j]
else:
K[i][j] = max(val[i-1]+ K[i-1][j-wt[i-1]], K[i-1][j])
return K[n][C]
def knapSack(C, wt, val, n):
K = [[0 for j in range(C + 1)] for i in range(n + 1)]
for i in range(n + 1):
for j in range(C + 1):
if i == 0 or j == 0:
K[i][j] = 0
if j < wt[i-1]:
K[i][j] = K[i-1][j]
else:
K[i][j] = max(val[i-1]+ K[i-1][j-wt[i-1]], K[i-1][j])
return K[n][C]
Weighted Job Scheduling
You are given n jobs such that each job has start time, end time and profit. If you choose a job that ends at time X, you will be able to start another job that starts at time X. The task is to find the maximum profit you can earn by picking up some (or all) jobs, ensuring no two jobs overlap. This is one of those problems where you have a choice to either pick a job or leave it.
Step 1: Sort the array by their end_time (through binary search)
Step 2: Iterate the array from n-1th index to 0th index. At every index, we’ll have a choice to either schedule the job or not.
Step 3: Choose the maximum profit of including the job or excluding it
However, the time complexity of this naive way is O(n * (2^n)). And similar to the previous problem, there are overlapping sub-problems.
Time Complexity: O(n^2) >> (w/ binary search) = O(n * log n)
class Job:
def __init__(self, start, finish, weight):
self.start = start
self.finish = finish
self.weight = weight
def find_max_weight(jobs):
# Sort jobs based on finish times
jobs.sort(key=lambda job: job.finish)
n = len(jobs)
dp = [0] * n
for i in range(n):
dp[i] = jobs[i].weight
for i in range(1, n):
for j in range(i):
if jobs[j].finish <= jobs[i].start:
# for each job, check if including the 'j' jobs before it profits more than just completing the ith job
dp[i] = max(dp[i], dp[j] + jobs[i].weight)
return max(dp)
# Example usage
jobs = [Job(1, 3, 5), Job(2, 5, 6), Job(4, 6, 5), Job(6, 7, 4), Job(5, 8, 11), Job(7, 9, 2)]
print("Maximum Weight:", find_max_weight(jobs))
You are given n jobs such that each job has start time, end time and profit. If you choose a job that ends at time X, you will be able to start another job that starts at time X. The task is to find the maximum profit you can earn by picking up some (or all) jobs, ensuring no two jobs overlap. This is one of those problems where you have a choice to either pick a job or leave it.
Step 1: Sort the array by their end_time (through binary search)
Step 2: Iterate the array from n-1th index to 0th index. At every index, we’ll have a choice to either schedule the job or not.
Step 3: Choose the maximum profit of including the job or excluding it
However, the time complexity of this naive way is O(n * (2^n)). And similar to the previous problem, there are overlapping sub-problems.
Time Complexity: O(n^2) >> (w/ binary search) = O(n * log n)
class Job:
def __init__(self, start, finish, weight):
self.start = start
self.finish = finish
self.weight = weight
def find_max_weight(jobs):
# Sort jobs based on finish times
jobs.sort(key=lambda job: job.finish)
n = len(jobs)
dp = [0] * n
for i in range(n):
dp[i] = jobs[i].weight
for i in range(1, n):
for j in range(i):
if jobs[j].finish <= jobs[i].start:
# for each job, check if including the 'j' jobs before it profits more than just completing the ith job
dp[i] = max(dp[i], dp[j] + jobs[i].weight)
return max(dp)
# Example usage
jobs = [Job(1, 3, 5), Job(2, 5, 6), Job(4, 6, 5), Job(6, 7, 4), Job(5, 8, 11), Job(7, 9, 2)]
print("Maximum Weight:", find_max_weight(jobs))
Another Implementation of weighted job scheduling
# Importing the following module to sort array based on our custom comparison function
from functools import cmp_to_key
class Job:
def __init__(self, start, finish, profit):
self.start = start
self.finish = finish
self.profit = profit
# A utility function that is used for sorting events according to finish time
def jobComparator(s1, s2):
return s1.finish < s2.finish
# Find the latest job (in sorted array) that doesn't conflict with the job[i]. If there's none, return -1
def latestNonConflict(arr, i):
for j in range(i - 1, -1, -1):
if arr[j].finish <= arr[i - 1].start:
return j
return -1
def findMaxProfit(arr, n):
# Sort jobs according to finish time
arr = sorted(arr, key=cmp_to_key(jobComparator))
# table[i] stores the profit for jobs till arr[i] (including arr[i])
table = [None] * n
table[0] = arr[0].profit
for i in range(1, n):
# Find profit including the current job
inclProf = arr[i].profit
l = latestNonConflict(arr, i)
if l != -1:
inclProf += table[l]
# Store maximum of including or excluding
table[i] = max(inclProf, table[i - 1])
return table[n - 1]
from functools import cmp_to_key
class Job:
def __init__(self, start, finish, profit):
self.start = start
self.finish = finish
self.profit = profit
# A utility function that is used for sorting events according to finish time
def jobComparator(s1, s2):
return s1.finish < s2.finish
# Find the latest job (in sorted array) that doesn't conflict with the job[i]. If there's none, return -1
def latestNonConflict(arr, i):
for j in range(i - 1, -1, -1):
if arr[j].finish <= arr[i - 1].start:
return j
return -1
def findMaxProfit(arr, n):
# Sort jobs according to finish time
arr = sorted(arr, key=cmp_to_key(jobComparator))
# table[i] stores the profit for jobs till arr[i] (including arr[i])
table = [None] * n
table[0] = arr[0].profit
for i in range(1, n):
# Find profit including the current job
inclProf = arr[i].profit
l = latestNonConflict(arr, i)
if l != -1:
inclProf += table[l]
# Store maximum of including or excluding
table[i] = max(inclProf, table[i - 1])
return table[n - 1]
Floyd Warshall
Finds the shortest path between all the pairs of vertices in a weighted graph. Works for directed and undirected graphs, but not ones with negative cycles (where the sum of the edges in a cycle is negative). Below is an example.
1) Start with n x n matrix, A0 - where each element ( A0[i][j] ) represents the weight of a single edge from i -> j
2) Build matrix A1 from A0 - where each element is min( i->j , i->1->(~ some other vertices)->j ) *(1 is a vertex)
3) Perform step 2) for all n vertex to get the final matrix with lowest sum of edge weights between all the pairs
- Build each matrix from previous (A0 -> A1 -> A2 -> A3 ... )
Finds the shortest path between all the pairs of vertices in a weighted graph. Works for directed and undirected graphs, but not ones with negative cycles (where the sum of the edges in a cycle is negative). Below is an example.
1) Start with n x n matrix, A0 - where each element ( A0[i][j] ) represents the weight of a single edge from i -> j
2) Build matrix A1 from A0 - where each element is min( i->j , i->1->(~ some other vertices)->j ) *(1 is a vertex)
3) Perform step 2) for all n vertex to get the final matrix with lowest sum of edge weights between all the pairs
- Build each matrix from previous (A0 -> A1 -> A2 -> A3 ... )
# Floyd Warshall Algorithm in python - Time Complexity: O(V^3), Space Complexity: O(V^2)
INF = float('inf')
def floyd_warshall(graph):
n = len(graph)
dist = [[0 if i == j else INF for j in range(n)] for i in range(n)]
for u in range(n):
for v, weight in graph[u]:
dist[u][v] = weight
for k in range(n):
for i in range(n):
for j in range(n):
dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j])
return dist
# Example graph representation: adjacency list with weights
G = [
[(1, 3), (2, 6)],
[(2, 2)],
[]
]
floyd_warshall(G)
INF = float('inf')
def floyd_warshall(graph):
n = len(graph)
dist = [[0 if i == j else INF for j in range(n)] for i in range(n)]
for u in range(n):
for v, weight in graph[u]:
dist[u][v] = weight
for k in range(n):
for i in range(n):
for j in range(n):
dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j])
return dist
# Example graph representation: adjacency list with weights
G = [
[(1, 3), (2, 6)],
[(2, 2)],
[]
]
floyd_warshall(G)
Bellman-Ford
Given a graph and a source vertex src in graph, find shortest paths from src to all vertices in the given graph. The graph may contain negative weight edges. (but cannot include negative weighted cycle)
Below is an example
Given a graph and a source vertex src in graph, find shortest paths from src to all vertices in the given graph. The graph may contain negative weight edges. (but cannot include negative weighted cycle)
Below is an example
Time Complexity: O(V * E), Space Complexity: O(V)
def bellmanFord(V, edges, src): # each element of edges: [v0 (src)], [v1 (dest)], [wt of v0 -> v1]
# Step 1 - Creating a V sized array/list, and initializing it with a very big value.
INF = 999999999
dis = [INF for x in range(V)]
dis[src] = 0 # Since we're already at src
# Step 2 - For V-1 times, traverse over, all the edges and checking if a shorter path between any edge u to v is possible.
for _ in range(V-1):
for j in range(len(edges)):
s = edges[j][0] # Source vertex
d = edges[j][1] # destination vertex
wt = edges[j][2] # weight of edge from u to v
# Update dis[v] from u if it can be reached with lower weight
if(dis[s] != INF and dis[s] + wt < dis[d]):
dis[d] = dis[s] + wt
# Step 3 - Checking for negative edge weight cycle
for i in range(len(edges)):
s = edges[i][0]
d = edges[i][1]
wt = edges[i][2]
# If traversing again is reducing the cost then it can be reduced infinitely
if(dis[s] != INF and dis[s] + wt < dis[d]):
return []
return dis
def bellmanFord(V, edges, src): # each element of edges: [v0 (src)], [v1 (dest)], [wt of v0 -> v1]
# Step 1 - Creating a V sized array/list, and initializing it with a very big value.
INF = 999999999
dis = [INF for x in range(V)]
dis[src] = 0 # Since we're already at src
# Step 2 - For V-1 times, traverse over, all the edges and checking if a shorter path between any edge u to v is possible.
for _ in range(V-1):
for j in range(len(edges)):
s = edges[j][0] # Source vertex
d = edges[j][1] # destination vertex
wt = edges[j][2] # weight of edge from u to v
# Update dis[v] from u if it can be reached with lower weight
if(dis[s] != INF and dis[s] + wt < dis[d]):
dis[d] = dis[s] + wt
# Step 3 - Checking for negative edge weight cycle
for i in range(len(edges)):
s = edges[i][0]
d = edges[i][1]
wt = edges[i][2]
# If traversing again is reducing the cost then it can be reduced infinitely
if(dis[s] != INF and dis[s] + wt < dis[d]):
return []
return dis
Matrix Chain Multiplication
Given a sequence of matrices, find the most efficient way to multiply these matrices together. The problem is not actually to perform the multiplications, but merely to decide in which order to perform the multiplications. Because matrix multiplication is associative, no matter how we parenthesize the product, the result will be the same.
For ex: (ABC)D = (AB)(CD) = A(BCD) = ....
However, the order in which we parenthesize the product affects the number of simple arithmetic operations needed to compute the product, or the efficiency. For example, suppose A is a 10 × 30 matrix, B is a 30 × 5 matrix, and C is a 5 × 60 matrix. Then,
(AB)C = (10×30×5) + (10×5×60) = 1500 + 3000 = 4500 operations
A(BC) = (30×5×60) + (10×30×60) = 9000 + 18000 = 27000 operations.
We need to write a function MatrixChainOrder() that should return the minimum number of multiplications needed to multiply the chain. Below is an example
Input: p[] = {40, 20, 30, 10, 30}
Output: 26000
Explanation: (A(BC))D --> 20*30*10 + 40*20*10 + 40*10*30
Thinking Process
A simple solution is to place parenthesis at all possible places, calculate the cost for each placement and return the minimum value. In a chain of matrices of size n, we can place the first set of parenthesis in n-1 ways.
For ex: ABCD => (A)(BCD), (AB)(CD) and (ABC)(D)
So, Minimum number of multiplication needed to multiply a chain of size n = Minimum of all n-1 placements (these placements create subproblems of smaller size). However, the time complexity of this is exponential.
This can be optimized by using memoization. For example, p = [1, 2, 3, 4, 3] will have some overlapping sub-problems
Given a sequence of matrices, find the most efficient way to multiply these matrices together. The problem is not actually to perform the multiplications, but merely to decide in which order to perform the multiplications. Because matrix multiplication is associative, no matter how we parenthesize the product, the result will be the same.
For ex: (ABC)D = (AB)(CD) = A(BCD) = ....
However, the order in which we parenthesize the product affects the number of simple arithmetic operations needed to compute the product, or the efficiency. For example, suppose A is a 10 × 30 matrix, B is a 30 × 5 matrix, and C is a 5 × 60 matrix. Then,
(AB)C = (10×30×5) + (10×5×60) = 1500 + 3000 = 4500 operations
A(BC) = (30×5×60) + (10×30×60) = 9000 + 18000 = 27000 operations.
We need to write a function MatrixChainOrder() that should return the minimum number of multiplications needed to multiply the chain. Below is an example
Input: p[] = {40, 20, 30, 10, 30}
Output: 26000
Explanation: (A(BC))D --> 20*30*10 + 40*20*10 + 40*10*30
Thinking Process
A simple solution is to place parenthesis at all possible places, calculate the cost for each placement and return the minimum value. In a chain of matrices of size n, we can place the first set of parenthesis in n-1 ways.
For ex: ABCD => (A)(BCD), (AB)(CD) and (ABC)(D)
So, Minimum number of multiplication needed to multiply a chain of size n = Minimum of all n-1 placements (these placements create subproblems of smaller size). However, the time complexity of this is exponential.
This can be optimized by using memoization. For example, p = [1, 2, 3, 4, 3] will have some overlapping sub-problems
Time Complexity: O(n^3), Space Complexity: O(n^2)
def matrix_chain_multiplication(dims):
n = len(dims) - 1 # Number of matrices
dp = [[0] * n for _ in range(n)]
for length in range(2, n + 1):
for i in range(n - length + 1):
j = i + length - 1
dp[i][j] = float('inf')
for k in range(i, j):
cost = dp[i][k] + dp[k + 1][j] + dims[i] * dims[k + 1] * dims[j + 1]
dp[i][j] = min(dp[i][j], cost)
return dp[0][n - 1]
# Example usage
matrix_dimensions = [10, 30, 5, 60]
minimum_scalar_multiplications = matrix_chain_multiplication(matrix_dimensions)
print("Minimum scalar multiplications:", minimum_scalar_multiplications)
def matrix_chain_multiplication(dims):
n = len(dims) - 1 # Number of matrices
dp = [[0] * n for _ in range(n)]
for length in range(2, n + 1):
for i in range(n - length + 1):
j = i + length - 1
dp[i][j] = float('inf')
for k in range(i, j):
cost = dp[i][k] + dp[k + 1][j] + dims[i] * dims[k + 1] * dims[j + 1]
dp[i][j] = min(dp[i][j], cost)
return dp[0][n - 1]
# Example usage
matrix_dimensions = [10, 30, 5, 60]
minimum_scalar_multiplications = matrix_chain_multiplication(matrix_dimensions)
print("Minimum scalar multiplications:", minimum_scalar_multiplications)
Greedy
Always selects the best option available at the moment and does not change an earlier decision. It works in a top-down approach. This may not produce the best result for all the problems since it always goes for the local best choice to get the global best result.
A greedy problem needs to have 2 properties:
1) Greedy Choice Property - If an optimal solution to the problem can be found by choosing the best choice at each step without reconsidering the previous steps once chosen
2) Optimal Substructure - If the optimal solution of the overall problem corresponds to the optimal solution of its subproblems
A greedy problem needs to have 2 properties:
1) Greedy Choice Property - If an optimal solution to the problem can be found by choosing the best choice at each step without reconsidering the previous steps once chosen
2) Optimal Substructure - If the optimal solution of the overall problem corresponds to the optimal solution of its subproblems
Coin Change
Problem: You have to make a change of an amount using the smallest possible number of coins.
Amount: $18
Available coins are: $5 coin $2 coin $1 coin
There is no limit to the number of each coin you can use.
Solution:
Problem: You have to make a change of an amount using the smallest possible number of coins.
Amount: $18
Available coins are: $5 coin $2 coin $1 coin
There is no limit to the number of each coin you can use.
Solution:
- Always select the largest value coin (i.e. 5) until sum > 18. (Selecting the largest value at each step, helps to reach the destination faster. => greedy choice property.)
- In 4th iteration, solution-set = {5, 5, 5, 2} and sum = 17. (Cannot select 5 here because then => sum = 20 which is greater than 18. So, we select the 2nd largest coin-value 2.)
- Similarly, in the fifth iteration, select 1. Now sum = 18 and solution-set = {5, 5, 5, 2, 1}.
Huffman Coding
A data-compression technique to reduce size without losing any details. Useful when there are frequently occurring characters.
For ex:- BCAADDDCCACACAC
Each character takes up 8 bits. So total = 8 * 15 = 120 bits
1. initiate a priority queue 'Q' consisting of unique characters.
2. sort the priority queue according to the ascending order of frequencies
3. for all the unique characters inside the queue:
- Initialize a new Node 'a'
- Return the minimum value of Q and assign it to the left child of 'a'
- Return the next minimum value of Q and assign it to the right Child of 'a'
- Find the sum of both returned values and assign it as the value of 'a'
- Insert the value of 'a' into the tree
4. repeat the same process until all unique characters of 'Q' are visited
5. Return root node
A data-compression technique to reduce size without losing any details. Useful when there are frequently occurring characters.
For ex:- BCAADDDCCACACAC
Each character takes up 8 bits. So total = 8 * 15 = 120 bits
1. initiate a priority queue 'Q' consisting of unique characters.
2. sort the priority queue according to the ascending order of frequencies
3. for all the unique characters inside the queue:
- Initialize a new Node 'a'
- Return the minimum value of Q and assign it to the left child of 'a'
- Return the next minimum value of Q and assign it to the right Child of 'a'
- Find the sum of both returned values and assign it as the value of 'a'
- Insert the value of 'a' into the tree
4. repeat the same process until all unique characters of 'Q' are visited
5. Return root node
Without encoding, total size was 120 bits.
After encoding total size is = 32 + 15 + 28 = 75.
Time Complexity: O(n * log n), Space Complexity:-
After encoding total size is = 32 + 15 + 28 = 75.
Time Complexity: O(n * log n), Space Complexity:-
from collections import Counter
class NodeTree(object):
def __init__(self, left=None, right=None):
self.left = left
self.right = right
def children(self):
return self.left, self.right
def __str__(self):
return self.left, self.right
# Given a NodeTree, returns a dictionary w/ chars as key and binary code as value
def huffman_code_tree(node, binString=''):
if type(node) is str:
return {node: binString}
(l, r) = node.children()
d = dict()
d.update(huffman_code_tree(l, binString + '0'))
d.update(huffman_code_tree(r, binString + '1'))
return d
# Builds tree, given a list of [(characters, frequency)], it returns the root of NodeTree
def make_tree(nodes):
while len(nodes) > 1:
(key1, c1) = nodes[-1]
(key2, c2) = nodes[-2]
nodes = nodes[:-2]
node = NodeTree(key1, key2)
nodes.append((node, c1 + c2))
nodes = sorted(nodes, key=lambda x: x[1], reverse=True)
return nodes[0][0]
if __name__ == '__main__':
string = 'BCAADDDCCACACAC'
freq = dict(Counter(string))
freq = sorted(freq.items(), key=lambda x: x[1], reverse=True)
node = make_tree(freq)
encoding = huffman_code_tree(node)
for i in encoding:
print(f'{i} : {encoding[i]}')
class NodeTree(object):
def __init__(self, left=None, right=None):
self.left = left
self.right = right
def children(self):
return self.left, self.right
def __str__(self):
return self.left, self.right
# Given a NodeTree, returns a dictionary w/ chars as key and binary code as value
def huffman_code_tree(node, binString=''):
if type(node) is str:
return {node: binString}
(l, r) = node.children()
d = dict()
d.update(huffman_code_tree(l, binString + '0'))
d.update(huffman_code_tree(r, binString + '1'))
return d
# Builds tree, given a list of [(characters, frequency)], it returns the root of NodeTree
def make_tree(nodes):
while len(nodes) > 1:
(key1, c1) = nodes[-1]
(key2, c2) = nodes[-2]
nodes = nodes[:-2]
node = NodeTree(key1, key2)
nodes.append((node, c1 + c2))
nodes = sorted(nodes, key=lambda x: x[1], reverse=True)
return nodes[0][0]
if __name__ == '__main__':
string = 'BCAADDDCCACACAC'
freq = dict(Counter(string))
freq = sorted(freq.items(), key=lambda x: x[1], reverse=True)
node = make_tree(freq)
encoding = huffman_code_tree(node)
for i in encoding:
print(f'{i} : {encoding[i]}')
* Minimum Spanning Tree (MST) - A graph that connects all vertices with a set of minimum-weighted edges. An MST has V-1 total edges
Dijkstra's
Find the shortest weighted-distance between 2 given vertices (unlike MST) does not have to go through every vertex.
Steps
1) Mark the value of the starting node as 0 and all the others as inf
2) Visit all the adjacent node and update its value by adding the weight of the edge
(if there's more than 1 path to a vertex, choose the lower value)
3) Perform step 2) on all connected vertices to get the shortest weighted distance
Application: Used in GPS devices and other network models.
Time Complexity: (w/ minimum priority queue) O(E log V) else O(V^2), Space Complexity: O(V)
Find the shortest weighted-distance between 2 given vertices (unlike MST) does not have to go through every vertex.
Steps
1) Mark the value of the starting node as 0 and all the others as inf
2) Visit all the adjacent node and update its value by adding the weight of the edge
(if there's more than 1 path to a vertex, choose the lower value)
3) Perform step 2) on all connected vertices to get the shortest weighted distance
Application: Used in GPS devices and other network models.
Time Complexity: (w/ minimum priority queue) O(E log V) else O(V^2), Space Complexity: O(V)
import math
graph = {'a':{'b':5,'c':2},
'b':{'a':5,'c':7,'d':8},
'c':{'a':2,'b':7,'d':4,'e':8},
'd':{'b':8,'c':4,'e':6, 'f':4},
'e':{'c':8,'d':6,'f':3},
'f':{'e':3, 'd':4}}
source = 'a'
destination = 'f'
unvisited = graph # add all nodes of graph to unvisited
shortest_distances = {}
route = []
path_nodes = {}
# set the distance of all nodes to inf and src to 0
for nodes in unvisited:
shortest_distances[nodes] = math.inf
shortest_distances[source] = 0
while(unvisited):
min_node = None
# for each node find the node that is unvisited and can be reached with the lowest weight
for current_node in unvisited:
if min_node is None:
min_node = current_node
elif shortest_distances[min_node] > shortest_distances[current_node]:
min_node = current_node
# for each node connected to the current min_node, update its distance if it can be reached through curr min_node with lower weight
for node,value in unvisited[min_node].items():
if value + shortest_distances[min_node] < shortest_distances[node]:
shortest_distances[node] = value + shortest_distances[min_node]
path_nodes[node] = min_node
# remove the curr min_node from unvisited
unvisited.pop(min_node)
graph = {'a':{'b':5,'c':2},
'b':{'a':5,'c':7,'d':8},
'c':{'a':2,'b':7,'d':4,'e':8},
'd':{'b':8,'c':4,'e':6, 'f':4},
'e':{'c':8,'d':6,'f':3},
'f':{'e':3, 'd':4}}
source = 'a'
destination = 'f'
unvisited = graph # add all nodes of graph to unvisited
shortest_distances = {}
route = []
path_nodes = {}
# set the distance of all nodes to inf and src to 0
for nodes in unvisited:
shortest_distances[nodes] = math.inf
shortest_distances[source] = 0
while(unvisited):
min_node = None
# for each node find the node that is unvisited and can be reached with the lowest weight
for current_node in unvisited:
if min_node is None:
min_node = current_node
elif shortest_distances[min_node] > shortest_distances[current_node]:
min_node = current_node
# for each node connected to the current min_node, update its distance if it can be reached through curr min_node with lower weight
for node,value in unvisited[min_node].items():
if value + shortest_distances[min_node] < shortest_distances[node]:
shortest_distances[node] = value + shortest_distances[min_node]
path_nodes[node] = min_node
# remove the curr min_node from unvisited
unvisited.pop(min_node)
Implementation of Dijkstra 2
# Uses adjacency matrix representation of the graph
class Graph():
def __init__(self, vertices):
self.V = vertices
self.graph = [[0 for column in range(vertices)]
for row in range(vertices)]
def printSolution(self, dist):
print("Vertex \t Distance from Source")
for node in range(self.V):
print(node, "\t\t", dist[node])
# A utility function to find the vertex with minimum distance value,
# from the set of vertices not yet included in shortest path tree (unvisited vertices)
def minDistance(self, dist, sptSet):
# Initialize minimum distance for next node
min = 1e7
for v in range(self.V):
if dist[v] < min and sptSet[v] == False:
min = dist[v]
min_index = v
return min_index
def dijkstra(self, src):
dist = [1e7] * self.V
dist[src] = 0
sptSet = [False] * self.V # Keeps track of visited vertices
for cout in range(self.V):
# Pick the minimum distance vertex from the set of unvisited vertices
# u is always equal to src in first iteration
u = self.minDistance(dist, sptSet)
# Put the minimum distance vertex in the shortest path tree
sptSet[u] = True
# Update dist value of the adjacent vertices of the picked vertex only
# if the old distance is greater than new distance and
# the vertex is not in the shortest path tree
for v in range(self.V):
if (self.graph[u][v] > 0 and
sptSet[v] == False and
dist[v] > dist[u] + self.graph[u][v]):
dist[v] = dist[u] + self.graph[u][v]
self.printSolution(dist)
# Driver program
g = Graph(9)
g.graph = [[0, 4, 0, 0, 0, 0, 0, 8, 0],
[4, 0, 8, 0, 0, 0, 0, 11, 0],
[0, 8, 0, 7, 0, 4, 0, 0, 2],
[0, 0, 7, 0, 9, 14, 0, 0, 0],
[0, 0, 0, 9, 0, 10, 0, 0, 0],
[0, 0, 4, 14, 10, 0, 2, 0, 0],
[0, 0, 0, 0, 0, 2, 0, 1, 6],
[8, 11, 0, 0, 0, 0, 1, 0, 7],
[0, 0, 2, 0, 0, 0, 6, 7, 0]]
g.dijkstra(0)
class Graph():
def __init__(self, vertices):
self.V = vertices
self.graph = [[0 for column in range(vertices)]
for row in range(vertices)]
def printSolution(self, dist):
print("Vertex \t Distance from Source")
for node in range(self.V):
print(node, "\t\t", dist[node])
# A utility function to find the vertex with minimum distance value,
# from the set of vertices not yet included in shortest path tree (unvisited vertices)
def minDistance(self, dist, sptSet):
# Initialize minimum distance for next node
min = 1e7
for v in range(self.V):
if dist[v] < min and sptSet[v] == False:
min = dist[v]
min_index = v
return min_index
def dijkstra(self, src):
dist = [1e7] * self.V
dist[src] = 0
sptSet = [False] * self.V # Keeps track of visited vertices
for cout in range(self.V):
# Pick the minimum distance vertex from the set of unvisited vertices
# u is always equal to src in first iteration
u = self.minDistance(dist, sptSet)
# Put the minimum distance vertex in the shortest path tree
sptSet[u] = True
# Update dist value of the adjacent vertices of the picked vertex only
# if the old distance is greater than new distance and
# the vertex is not in the shortest path tree
for v in range(self.V):
if (self.graph[u][v] > 0 and
sptSet[v] == False and
dist[v] > dist[u] + self.graph[u][v]):
dist[v] = dist[u] + self.graph[u][v]
self.printSolution(dist)
# Driver program
g = Graph(9)
g.graph = [[0, 4, 0, 0, 0, 0, 0, 8, 0],
[4, 0, 8, 0, 0, 0, 0, 11, 0],
[0, 8, 0, 7, 0, 4, 0, 0, 2],
[0, 0, 7, 0, 9, 14, 0, 0, 0],
[0, 0, 0, 9, 0, 10, 0, 0, 0],
[0, 0, 4, 14, 10, 0, 2, 0, 0],
[0, 0, 0, 0, 0, 2, 0, 1, 6],
[8, 11, 0, 0, 0, 0, 1, 0, 7],
[0, 0, 2, 0, 0, 0, 6, 7, 0]]
g.dijkstra(0)
IMPLEMENTATION OF DIJKSTRA 3
from heapq import heappop, heappush
INF = float('inf')
def dijkstra(graph, source):
n = len(graph)
distances = [INF] * n
distances[source] = 0
visited = [False] * n
heap = [(0, source)]
while heap:
dist, node = heappop(heap)
visited[node] = True
for neighbor, weight in graph[node]:
if not visited[neighbor] and dist + weight < distances[neighbor]:
distances[neighbor] = dist + weight
heappush(heap, (distances[neighbor], neighbor))
return distances
# Example graph representation: adjacency list with weights
graph = [
[(1, 4), (2, 1)],
[(2, 3), (3, 2)],
[(3, 5)],
[]
]
source_vertex = 0
shortest_distances = dijkstra(graph, source_vertex)
print("Shortest distances from source vertex", source_vertex)
for idx, distance in enumerate(shortest_distances):
print(f"Vertex {idx}: {distance}")
INF = float('inf')
def dijkstra(graph, source):
n = len(graph)
distances = [INF] * n
distances[source] = 0
visited = [False] * n
heap = [(0, source)]
while heap:
dist, node = heappop(heap)
visited[node] = True
for neighbor, weight in graph[node]:
if not visited[neighbor] and dist + weight < distances[neighbor]:
distances[neighbor] = dist + weight
heappush(heap, (distances[neighbor], neighbor))
return distances
# Example graph representation: adjacency list with weights
graph = [
[(1, 4), (2, 1)],
[(2, 3), (3, 2)],
[(3, 5)],
[]
]
source_vertex = 0
shortest_distances = dijkstra(graph, source_vertex)
print("Shortest distances from source vertex", source_vertex)
for idx, distance in enumerate(shortest_distances):
print(f"Vertex {idx}: {distance}")
Kruskal's Algorithm
Given a graph find the MST
Time Complexity: O(E * log E), Space Complexity: O(V + E)
class DisjointSet:
def __init__(self, n):
self.parent = list(range(n)) # Initialize parent pointers
self.rank = [0] * n # Initialize ranks
# The purpose of this code is to find the representative (also known as the main root) of a given element x in the disjoint-set.
def find(self, x):
if self.parent[x] != x:
self.parent[x] = self.find(self.parent[x]) # Path compression
return self.parent[x]
# Union: merges 2 disjoint sets - finds the least weighted edge that connects the 2 disjoint set
def union(self, x, y):
root_x = self.find(x)
root_y = self.find(y)
if root_x != root_y:
if self.rank[root_x] > self.rank[root_y]:
self.parent[root_y] = root_x # Attach smaller rank tree under root of higher rank tree
else:
self.parent[root_x] = root_y
if self.rank[root_x] == self.rank[root_y]:
self.rank[root_y] += 1
def kruskal(graph, n):
graph.sort(key=lambda edge: edge[2]) # Sort edges by weight - lowest to highest
disjoint_set = DisjointSet(n) # Initialize disjoint-set data structure
minimum_spanning_tree = [] # To store the selected edges of the MST
# for each edge in graph from lowest to highest -
for u, v, weight in graph:
# This condition checks whether adding the current edge (u, v) to the MST would create a cycle. It does this by checking if the parent (root) of vertex u is different from the parent (root) of vertex v in the disjoint-set data structure. If they have different parents, it means that adding this edge won't form a cycle.
if disjoint_set.find(u) != disjoint_set.find(v):
disjoint_set.union(u, v) # Union two sets if they are not connected
minimum_spanning_tree.append((u, v, weight))
return minimum_spanning_tree
# Example graph representation: list of edges with weights
graph = [
(0, 1, 4),
(0, 7, 8),
(1, 7, 11),
(1, 2, 8),
(2, 8, 2),
(2, 3, 7),
(2, 5, 4),
(3, 5, 14),
(3, 4, 9),
(4, 5, 10),
(5, 6, 2),
(6, 8, 6),
(6, 7, 1),
(7, 8, 7)
]
num_vertices = 9
minimum_spanning_tree = kruskal(graph, num_vertices)
print("Minimum Spanning Tree:")
for u, v, weight in minimum_spanning_tree:
print(f"Edge: ({u}, {v}), Weight: {weight}")
Given a graph find the MST
- 1) Sort all the edges from low weight to high
- 2) Take the edge with the lowest weight and add it to the spanning tree. If adding the edge created a cycle, then reject this edge.
- 3) Keep adding edges until we reach all vertices.
Time Complexity: O(E * log E), Space Complexity: O(V + E)
class DisjointSet:
def __init__(self, n):
self.parent = list(range(n)) # Initialize parent pointers
self.rank = [0] * n # Initialize ranks
# The purpose of this code is to find the representative (also known as the main root) of a given element x in the disjoint-set.
def find(self, x):
if self.parent[x] != x:
self.parent[x] = self.find(self.parent[x]) # Path compression
return self.parent[x]
# Union: merges 2 disjoint sets - finds the least weighted edge that connects the 2 disjoint set
def union(self, x, y):
root_x = self.find(x)
root_y = self.find(y)
if root_x != root_y:
if self.rank[root_x] > self.rank[root_y]:
self.parent[root_y] = root_x # Attach smaller rank tree under root of higher rank tree
else:
self.parent[root_x] = root_y
if self.rank[root_x] == self.rank[root_y]:
self.rank[root_y] += 1
def kruskal(graph, n):
graph.sort(key=lambda edge: edge[2]) # Sort edges by weight - lowest to highest
disjoint_set = DisjointSet(n) # Initialize disjoint-set data structure
minimum_spanning_tree = [] # To store the selected edges of the MST
# for each edge in graph from lowest to highest -
for u, v, weight in graph:
# This condition checks whether adding the current edge (u, v) to the MST would create a cycle. It does this by checking if the parent (root) of vertex u is different from the parent (root) of vertex v in the disjoint-set data structure. If they have different parents, it means that adding this edge won't form a cycle.
if disjoint_set.find(u) != disjoint_set.find(v):
disjoint_set.union(u, v) # Union two sets if they are not connected
minimum_spanning_tree.append((u, v, weight))
return minimum_spanning_tree
# Example graph representation: list of edges with weights
graph = [
(0, 1, 4),
(0, 7, 8),
(1, 7, 11),
(1, 2, 8),
(2, 8, 2),
(2, 3, 7),
(2, 5, 4),
(3, 5, 14),
(3, 4, 9),
(4, 5, 10),
(5, 6, 2),
(6, 8, 6),
(6, 7, 1),
(7, 8, 7)
]
num_vertices = 9
minimum_spanning_tree = kruskal(graph, num_vertices)
print("Minimum Spanning Tree:")
for u, v, weight in minimum_spanning_tree:
print(f"Edge: ({u}, {v}), Weight: {weight}")
Another implementation of kruskal
from collections import defaultdict
class Graph:
def __init__(self, vertices):
self.V = vertices # No. of vertices
self.graph = [] # default dictionary to store graph
def addEdge(self, u, v, w):
self.graph.append([u, v, w])
def find(self, parent, i):
if parent[i] == i:
return i
return self.find(parent, parent[i])
# A function that does union of two sets of x and y (uses union by rank)
def union(self, parent, rank, x, y):
xroot = self.find(parent, x)
yroot = self.find(parent, y)
# Attach smaller rank tree under root of high rank tree (Union by Rank)
if rank[xroot] < rank[yroot]:
parent[xroot] = yroot
elif rank[xroot] > rank[yroot]:
parent[yroot] = xroot
# If ranks are same, then make one as root and increment its rank by one
else:
parent[yroot] = xroot
rank[xroot] += 1
# The main function to construct MST using Kruskal's algorithm
def KruskalMST(self):
result = [] # This will store the resultant MST
# An index variable, used for sorted edges
i = 0
# An index variable, used for result[]
e = 0
# Step 1: Sort all the edges in non-decreasing order of their weight
self.graph = sorted(self.graph, key=lambda item: item[2])
parent = []
rank = []
# Create V subsets with single elements
for node in range(self.V):
parent.append(node)
rank.append(0)
# Number of edges to be taken is equal to V-1
while e < self.V - 1:
# Step 2: Pick the smallest edge and increment the index for next iteration
u, v, w = self.graph[i]
i = i + 1
x = self.find(parent, u)
y = self.find(parent, v)
# If including this edge doesn't cause cycle, then include it in result
# and increment the index of result for next edge
if x != y:
e = e + 1
result.append([u, v, w])
self.union(parent, rank, x, y)
# else discard the edge
class Graph:
def __init__(self, vertices):
self.V = vertices # No. of vertices
self.graph = [] # default dictionary to store graph
def addEdge(self, u, v, w):
self.graph.append([u, v, w])
def find(self, parent, i):
if parent[i] == i:
return i
return self.find(parent, parent[i])
# A function that does union of two sets of x and y (uses union by rank)
def union(self, parent, rank, x, y):
xroot = self.find(parent, x)
yroot = self.find(parent, y)
# Attach smaller rank tree under root of high rank tree (Union by Rank)
if rank[xroot] < rank[yroot]:
parent[xroot] = yroot
elif rank[xroot] > rank[yroot]:
parent[yroot] = xroot
# If ranks are same, then make one as root and increment its rank by one
else:
parent[yroot] = xroot
rank[xroot] += 1
# The main function to construct MST using Kruskal's algorithm
def KruskalMST(self):
result = [] # This will store the resultant MST
# An index variable, used for sorted edges
i = 0
# An index variable, used for result[]
e = 0
# Step 1: Sort all the edges in non-decreasing order of their weight
self.graph = sorted(self.graph, key=lambda item: item[2])
parent = []
rank = []
# Create V subsets with single elements
for node in range(self.V):
parent.append(node)
rank.append(0)
# Number of edges to be taken is equal to V-1
while e < self.V - 1:
# Step 2: Pick the smallest edge and increment the index for next iteration
u, v, w = self.graph[i]
i = i + 1
x = self.find(parent, u)
y = self.find(parent, v)
# If including this edge doesn't cause cycle, then include it in result
# and increment the index of result for next edge
if x != y:
e = e + 1
result.append([u, v, w])
self.union(parent, rank, x, y)
# else discard the edge
Prim's Algorithm
Given a graph find the MST
Time Complexity: O(V^2), Space Complexity: O(V)
from heapq import heappop, heappush
def prim(graph, start):
n = len(graph)
visited = [False] * n
min_heap = [(0, start)] # Heap of (weight, vertex) pairs
minimum_spanning_tree = []
while min_heap:
weight, node = heappop(min_heap)
if visited[node]:
continue
visited[node] = True
for neighbor, edge_weight in graph[node]:
if not visited[neighbor]:
heappush(min_heap, (edge_weight, neighbor))
if node != start: # Skip the start node
minimum_spanning_tree.append((node, weight))
return minimum_spanning_tree
# Example graph representation: adjacency list with weights
graph = [
[(1, 4), (7, 8)],
[(0, 4), (7, 11), (2, 8)],
[(1, 8), (8, 2), (3, 7), (5, 4)],
[(2, 7), (5, 14), (4, 9)],
[(3, 9), (5, 10)],
[(2, 4), (3, 14), (4, 10), (6, 2)],
[(5, 2), (8, 6), (7, 1)],
[(0, 8), (1, 11), (6, 1), (8, 7)],
[(2, 2), (6, 6), (7, 7)]
]
start_vertex = 0
minimum_spanning_tree = prim(graph, start_vertex)
print("Minimum Spanning Tree:")
for node, weight in minimum_spanning_tree:
print(f"Edge: ({start_vertex}, {node}), Weight: {weight}")
Given a graph find the MST
- 1) Initialize the minimum spanning tree with a vertex chosen at random and add it to the tree.
- 2) Find an minimum weight edges that connect the tree to a new vertices (not already in the tree)
- 3) Keep repeating step 2 until we get a minimum spanning tree (when all vertices become part of the tree)
Time Complexity: O(V^2), Space Complexity: O(V)
from heapq import heappop, heappush
def prim(graph, start):
n = len(graph)
visited = [False] * n
min_heap = [(0, start)] # Heap of (weight, vertex) pairs
minimum_spanning_tree = []
while min_heap:
weight, node = heappop(min_heap)
if visited[node]:
continue
visited[node] = True
for neighbor, edge_weight in graph[node]:
if not visited[neighbor]:
heappush(min_heap, (edge_weight, neighbor))
if node != start: # Skip the start node
minimum_spanning_tree.append((node, weight))
return minimum_spanning_tree
# Example graph representation: adjacency list with weights
graph = [
[(1, 4), (7, 8)],
[(0, 4), (7, 11), (2, 8)],
[(1, 8), (8, 2), (3, 7), (5, 4)],
[(2, 7), (5, 14), (4, 9)],
[(3, 9), (5, 10)],
[(2, 4), (3, 14), (4, 10), (6, 2)],
[(5, 2), (8, 6), (7, 1)],
[(0, 8), (1, 11), (6, 1), (8, 7)],
[(2, 2), (6, 6), (7, 7)]
]
start_vertex = 0
minimum_spanning_tree = prim(graph, start_vertex)
print("Minimum Spanning Tree:")
for node, weight in minimum_spanning_tree:
print(f"Edge: ({start_vertex}, {node}), Weight: {weight}")
Another implementation of Prim's
INF = 9999999
V = 5 # number of vertices in graph
G = [[0, 9, 75, 0, 0],
[9, 0, 95, 19, 42],
[75, 95, 0, 51, 66],
[0, 19, 51, 0, 31],
[0, 42, 66, 31, 0]]
# create an array to track selected vertex
selected = [False] * V
no_edge = 0
# choose a random starting point
selected[0] = True
print("Edge : Weight\n")
while (no_edge < V - 1):
# For every vertex in the set S, find the all adjacent vertices,
# calculate the distance from the vertex selected at step 1.
# if the vertex is already in the set S, discard it otherwise
# choose another vertex nearest to selected vertex at step 1.
minimum = INF
x = 0
y = 0
for i in range(V):
if selected[i]:
for j in range(V):
if ((not selected[j]) and G[i][j]):
# not in selected and there is an edge
if minimum > G[i][j]:
minimum = G[i][j]
x = i
y = j
print(str(x) + "-" + str(y) + ":" + str(G[x][y]))
selected[y] = True
no_edge += 1
V = 5 # number of vertices in graph
G = [[0, 9, 75, 0, 0],
[9, 0, 95, 19, 42],
[75, 95, 0, 51, 66],
[0, 19, 51, 0, 31],
[0, 42, 66, 31, 0]]
# create an array to track selected vertex
selected = [False] * V
no_edge = 0
# choose a random starting point
selected[0] = True
print("Edge : Weight\n")
while (no_edge < V - 1):
# For every vertex in the set S, find the all adjacent vertices,
# calculate the distance from the vertex selected at step 1.
# if the vertex is already in the set S, discard it otherwise
# choose another vertex nearest to selected vertex at step 1.
minimum = INF
x = 0
y = 0
for i in range(V):
if selected[i]:
for j in range(V):
if ((not selected[j]) and G[i][j]):
# not in selected and there is an edge
if minimum > G[i][j]:
minimum = G[i][j]
x = i
y = j
print(str(x) + "-" + str(y) + ":" + str(G[x][y]))
selected[y] = True
no_edge += 1
Fractional Knapsack problem
Same as 0/1 Knapsack except, we can break items for maximizing the total value of the knapsack.
Time Complexity: O(n * log n), Space Complexity: O(n)
# Structure for an item which stores weight and
# corresponding value of Item
class Item:
def __init__(self, value, weight):
self.value = value
self.weight = weight
def fractionalKnapsack(W, arr):
# sorting Item on basis of ratio
arr.sort(key=lambda x: (x.value/x.weight), reverse=True)
finalvalue = 0.0
for item in arr:
# If adding Item won't overflow, add it completely
if item.weight <= W:
W -= item.weight
finalvalue += item.value
# If we can't add current Item, add fractional part of it
else:
finalvalue += item.value * W / item.weight
break
return finalvalue
Same as 0/1 Knapsack except, we can break items for maximizing the total value of the knapsack.
- Calculate the ratio(value/weight) for each item.
- Sort all the items in decreasing order of the ratio.
- Initialize finalvalue = 0, curr_cap = given_cap.
- Do the following for every item “i” in the sorted order:
- If the weight of the current item is less than or equal to the remaining capacity then add the value of that item into the result
- else add the current item as much as we can and break out of the loop
- Return finalvalue
Time Complexity: O(n * log n), Space Complexity: O(n)
# Structure for an item which stores weight and
# corresponding value of Item
class Item:
def __init__(self, value, weight):
self.value = value
self.weight = weight
def fractionalKnapsack(W, arr):
# sorting Item on basis of ratio
arr.sort(key=lambda x: (x.value/x.weight), reverse=True)
finalvalue = 0.0
for item in arr:
# If adding Item won't overflow, add it completely
if item.weight <= W:
W -= item.weight
finalvalue += item.value
# If we can't add current Item, add fractional part of it
else:
finalvalue += item.value * W / item.weight
break
return finalvalue
Traveling Salesman Problem
Given a set of cities and distances between every pair of cities => Find shortest possible route that visits every city exactly once and returns to the starting point.
* The Hamiltonian cycle problem is to find if there exists a tour that visits every city exactly once. Here we know that at least one Hamiltonian Tour exists
Time Complexity: O((n^2) * log n), Space Complexity: O(n)
def tsp_greedy(graph, start):
n = len(graph)
visited = [False] * n # keep track of the visited nodes
tour = [start] # order of nodes visited
total_distance = 0
current_city = start
for _ in range(n - 1): # loop through until every n-1 nodes other than start node is visited
nearest_city = None
min_distance = float('inf')
# loop through all connected nodes to the current node and find the node that can be reached with the least distance
for next_city in range(n):
if not visited[next_city] and graph[current_city][next_city] < min_distance:
nearest_city = next_city
min_distance = graph[current_city][next_city]
tour.append(nearest_city)
total_distance += min_distance
visited[nearest_city] = True. # mark next city as visited for hamiltonian cycle or mark current city as visited for path
current_city = nearest_city # set next city in tour to the least distance node
# Return to the starting city
tour.append(start)
total_distance += graph[current_city][start]
return tour, total_distance
# Example graph representation: adjacency matrix with distances
graph = [
[0, 29, 20, 21],
[29, 0, 15, 18],
[20, 15, 0, 16],
[21, 18, 16, 0]
]
Given a set of cities and distances between every pair of cities => Find shortest possible route that visits every city exactly once and returns to the starting point.
* The Hamiltonian cycle problem is to find if there exists a tour that visits every city exactly once. Here we know that at least one Hamiltonian Tour exists
- 1. Create two primary data holders:
- - A list that holds the indices of the cities in terms of the input matrix of distances between cities.
- - Result array which will have all cities that can be displayed out to the console in any manner.
- 2. Perform traversal on the given adjacency matrix tsp[][] for all the city and if the cost of the reaching any city from current city is less than current cost the update the cost.
- 3. Generate the minimum path cycle using the above step and return there minimum cost.
Time Complexity: O((n^2) * log n), Space Complexity: O(n)
def tsp_greedy(graph, start):
n = len(graph)
visited = [False] * n # keep track of the visited nodes
tour = [start] # order of nodes visited
total_distance = 0
current_city = start
for _ in range(n - 1): # loop through until every n-1 nodes other than start node is visited
nearest_city = None
min_distance = float('inf')
# loop through all connected nodes to the current node and find the node that can be reached with the least distance
for next_city in range(n):
if not visited[next_city] and graph[current_city][next_city] < min_distance:
nearest_city = next_city
min_distance = graph[current_city][next_city]
tour.append(nearest_city)
total_distance += min_distance
visited[nearest_city] = True. # mark next city as visited for hamiltonian cycle or mark current city as visited for path
current_city = nearest_city # set next city in tour to the least distance node
# Return to the starting city
tour.append(start)
total_distance += graph[current_city][start]
return tour, total_distance
# Example graph representation: adjacency matrix with distances
graph = [
[0, 29, 20, 21],
[29, 0, 15, 18],
[20, 15, 0, 16],
[21, 18, 16, 0]
]
Travelling Salesman (using Tabulation - dynamic programming)
def tsp_tabulation(graph, n):
# Create a table to store subproblem solutions
dp = [[float('inf')] * (1 << n) for _ in range(n)]
# Initialize base cases: reaching a city from the starting city
for i in range(n):
dp[i][1 << i] = graph[i][0]
# Iterate over subsets of cities
for mask in range(1, 1 << n):
for u in range(n):
if (mask & (1 << u)) != 0:
for v in range(n):
if (mask & (1 << v)) != 0 and u != v:
dp[u][mask] = min(dp[u][mask], graph[u][v] + dp[v][mask ^ (1 << u)])
# Find the minimum cost of visiting all cities and returning to the starting city
min_cost = float('inf')
for v in range(1, n):
min_cost = min(min_cost, graph[0][v] + dp[v][(1 << n) - 1])
return min_cost
# Example graph representation: adjacency matrix with distances
graph = [
[0, 29, 20, 21],
[29, 0, 15, 18],
[20, 15, 0, 16],
[21, 18, 16, 0]
]
num_cities = len(graph)
min_cost = tsp_tabulation(graph, num_cities)
print("Minimum cost of TSP using tabulation:", min_cost)
# Create a table to store subproblem solutions
dp = [[float('inf')] * (1 << n) for _ in range(n)]
# Initialize base cases: reaching a city from the starting city
for i in range(n):
dp[i][1 << i] = graph[i][0]
# Iterate over subsets of cities
for mask in range(1, 1 << n):
for u in range(n):
if (mask & (1 << u)) != 0:
for v in range(n):
if (mask & (1 << v)) != 0 and u != v:
dp[u][mask] = min(dp[u][mask], graph[u][v] + dp[v][mask ^ (1 << u)])
# Find the minimum cost of visiting all cities and returning to the starting city
min_cost = float('inf')
for v in range(1, n):
min_cost = min(min_cost, graph[0][v] + dp[v][(1 << n) - 1])
return min_cost
# Example graph representation: adjacency matrix with distances
graph = [
[0, 29, 20, 21],
[29, 0, 15, 18],
[20, 15, 0, 16],
[21, 18, 16, 0]
]
num_cities = len(graph)
min_cost = tsp_tabulation(graph, num_cities)
print("Minimum cost of TSP using tabulation:", min_cost)
Vertex Cover
Time Complexity: O(V + E), Space Complexity: O(V)
def vertex_cover_greedy(graph):
vertex_cover = set() # Set to store selected vertices
edges = [(u, v) for u in range(len(graph)) for v in graph[u]] # List of edges
while edges:
# Select an edge with the maximum degree (an edge that is connected to the vertex with the highest degree)
max_degree_edge = max(edges, key=lambda edge: graph[edge[0]] + graph[edge[1]])
vertex_cover.update(max_degree_edge) # Add the vertices of the selected edge
# filters out edges from the edges list that contain vertex with the maximum degree
edges = [edge for edge in edges if max_degree_edge[0] not in edge and max_degree_edge[1] not in edge]
return vertex_cover
- Initialize the vertex cover set as empty.
- Let the set of all edges in the graph be called E.
- While E is not empty:
- Pick a random edge from the set E, add its constituent nodes, u and v into the vertex cover set.
- For all the edges, which have either u or v as their part, remove them from the set E.
- Return the final obtained vertex cover set, after the set E is empty.
Time Complexity: O(V + E), Space Complexity: O(V)
def vertex_cover_greedy(graph):
vertex_cover = set() # Set to store selected vertices
edges = [(u, v) for u in range(len(graph)) for v in graph[u]] # List of edges
while edges:
# Select an edge with the maximum degree (an edge that is connected to the vertex with the highest degree)
max_degree_edge = max(edges, key=lambda edge: graph[edge[0]] + graph[edge[1]])
vertex_cover.update(max_degree_edge) # Add the vertices of the selected edge
# filters out edges from the edges list that contain vertex with the maximum degree
edges = [edge for edge in edges if max_degree_edge[0] not in edge and max_degree_edge[1] not in edge]
return vertex_cover
Activity Selection Problem
Given n activities with their start and finish times. Select max # of activities that can be performed by a single person, assuming that a person can only work on a single activity at a time.
1) Sort the activities according to their finishing time
2) Select the first activity from the sorted array and print it.
3) Do the following for the remaining activities in the sorted array.
…….a) If the start time of this activity is greater than or equal to the finish time of the previously selected activity then select this activity and print it.
Time Complexity: O(n), Space Complexity: O(1)
def activity_selection(activities):
n = len(activities)
activities.sort(key=lambda x: x[1]) # Sort activities by finish time
selected_activities = [activities[0]]
last_selected = 0 # Index of the last selected activity
for i in range(1, n): # for each of the next selected activities check if its start time is after finish time of current activity
if activities[i][0] >= activities[last_selected][1]:
selected_activities.append(activities[i])
last_selected = i
return selected_activities
# Example activity representation: (start_time, finish_time)
activities = [
(1, 3), (2, 5), (3, 6), (5, 7), (8, 9), (10, 12)
]
selected_activities = activity_selection(activities)
print("Selected Activities:", selected_activities)
Given n activities with their start and finish times. Select max # of activities that can be performed by a single person, assuming that a person can only work on a single activity at a time.
1) Sort the activities according to their finishing time
2) Select the first activity from the sorted array and print it.
3) Do the following for the remaining activities in the sorted array.
…….a) If the start time of this activity is greater than or equal to the finish time of the previously selected activity then select this activity and print it.
Time Complexity: O(n), Space Complexity: O(1)
def activity_selection(activities):
n = len(activities)
activities.sort(key=lambda x: x[1]) # Sort activities by finish time
selected_activities = [activities[0]]
last_selected = 0 # Index of the last selected activity
for i in range(1, n): # for each of the next selected activities check if its start time is after finish time of current activity
if activities[i][0] >= activities[last_selected][1]:
selected_activities.append(activities[i])
last_selected = i
return selected_activities
# Example activity representation: (start_time, finish_time)
activities = [
(1, 3), (2, 5), (3, 6), (5, 7), (8, 9), (10, 12)
]
selected_activities = activity_selection(activities)
print("Selected Activities:", selected_activities)
Job Sequencing
Given an array of jobs with deadline and associated profit only if the job is finished before the deadline. It is also given that every job takes a single unit of time, so the minimum possible deadline for any job is 1. Maximize the total profit if only one job can be scheduled at a time.
Greedily choose the jobs with maximum profit first, by sorting the jobs in decreasing order of their profit. This would help to maximize the total profit as choosing the job with maximum profit for every time slot will eventually maximize the total profit
Time Complexity: O(n^2), Space Complexity: O(n)
# t = no. of jobs to schedule
def printJobScheduling(arr, t):
n = len(arr)
# Sort all jobs according to decreasing order of profit
for i in range(n):
for j in range(n - 1 - i):
if arr[j][2] < arr[j + 1][2]:
arr[j], arr[j + 1] = arr[j + 1], arr[j]
# To keep track of free time slots
result = [False] * t
# To store result (Sequence of jobs)
job = ['-1'] * t
# Iterate through all given jobs
for i in range(len(arr)):
# Find a free slot for this job
# (Note that we start from the last possible slot)
for j in range(min(t - 1, arr[i][1] - 1), -1, -1):
# Free slot found
if result[j] is False:
result[j] = True
job[j] = arr[i][0]
break
# print the sequence
print(job)
Given an array of jobs with deadline and associated profit only if the job is finished before the deadline. It is also given that every job takes a single unit of time, so the minimum possible deadline for any job is 1. Maximize the total profit if only one job can be scheduled at a time.
Greedily choose the jobs with maximum profit first, by sorting the jobs in decreasing order of their profit. This would help to maximize the total profit as choosing the job with maximum profit for every time slot will eventually maximize the total profit
- Sort all jobs in decreasing order of profit.
- Iterate on jobs in decreasing order of profit. For each job , do the following :
- - Find a time slot i, such that slot is empty and i < deadline and i is greatest. Put the job in this slot and mark this slot filled.
- - If no such i exists, then ignore the job.
Time Complexity: O(n^2), Space Complexity: O(n)
# t = no. of jobs to schedule
def printJobScheduling(arr, t):
n = len(arr)
# Sort all jobs according to decreasing order of profit
for i in range(n):
for j in range(n - 1 - i):
if arr[j][2] < arr[j + 1][2]:
arr[j], arr[j + 1] = arr[j + 1], arr[j]
# To keep track of free time slots
result = [False] * t
# To store result (Sequence of jobs)
job = ['-1'] * t
# Iterate through all given jobs
for i in range(len(arr)):
# Find a free slot for this job
# (Note that we start from the last possible slot)
for j in range(min(t - 1, arr[i][1] - 1), -1, -1):
# Free slot found
if result[j] is False:
result[j] = True
job[j] = arr[i][0]
break
# print the sequence
print(job)
Explanation
- arr is a list of jobs, where each job is represented as a tuple (job_id, deadline, profit).
- t is the total number of time slots available.
- 1. The code starts by sorting the list of jobs in decreasing order of profit. This is done using the bubble sort algorithm (not the most efficient method, but it suffices for demonstration purposes).
- 2. Two lists are initialized: result to keep track of free time slots and job to store the final sequence of jobs.
- 3. The code iterates through each job in the sorted order.
- 4. For each job, it tries to find a free time slot for scheduling the job. The loop starts from min(t - 1, arr[i][1] - 1) and iterates backward until it finds a free slot that doesn't violate the job's deadline.
- 5. Once a free slot is found, it updates the result list to mark the slot as occupied and assigns the job's ID to the corresponding slot in the job list.
- 6. Finally, the code prints the sequence of jobs in the order they are scheduled.
Ford Fulkerson
Given a graph which represents a flow network where every edge has a capacity. Also given two vertices source ‘s’ and sink ‘t’ in the graph, find the maximum possible flow from s to t with following constraints:
Time Complexity: O(max_flow * E), Space Complexity:-
from collections import defaultdict
class Graph:
def __init__(self, graph):
self.graph = graph # residual graph
self. ROW = len(graph)
# self.COL = len(gr[0])
'''Returns true if there is a path from source 's' to sink 't' in
residual graph. Also fills parent[] to store the path '''
def BFS(self, s, t, parent):
# Mark all the vertices as not visited
visited = [False]*(self.ROW)
# Create a queue for BFS
queue = []
# Mark the source node as visited and enqueue it
queue.append(s)
visited[s] = True
# Standard BFS Loop
while queue:
# Dequeue a vertex from queue and print it
u = queue.pop(0)
# Get all adjacent vertices of the dequeued vertex u
# If a adjacent has not been visited, then mark it visited and enqueue it
for ind, val in enumerate(self.graph[u]):
if visited[ind] == False and val > 0:
# If we find a connection to the sink node, then there is no point in BFS anymore
# We just have to set its parent and can return true
queue.append(ind)
visited[ind] = True
parent[ind] = u
if ind == t:
return True
# We didn't reach sink in BFS starting from source, so return false
return False
# Returns the maximum flow from s to t in the given graph
def FordFulkerson(self, source, sink):
# This array is filled by BFS and to store path
parent = [-1]*(self.ROW)
max_flow = 0 # There is no flow initially
# Augment the flow while there is path from source to sink
while self.BFS(source, sink, parent) :
# Find minimum residual capacity of the edges along the path filled by BFS.
# Or we can say find the maximum flow through the path found.
path_flow = float("Inf")
s = sink
while(s != source):
path_flow = min (path_flow, self.graph[parent[s]][s])
s = parent[s]
# Add path flow to overall flow
max_flow += path_flow
# update residual capacities of the edges and reverse edges along the path
v = sink
while(v != source):
u = parent[v]
self.graph[u][v] -= path_flow
self.graph[v][u] += path_flow
v = parent[v]
return max_flow
Given a graph which represents a flow network where every edge has a capacity. Also given two vertices source ‘s’ and sink ‘t’ in the graph, find the maximum possible flow from s to t with following constraints:
- Flow on an edge doesn’t exceed the given capacity of the edge.
- Incoming flow is equal to outgoing flow for every vertex except s and t.
Time Complexity: O(max_flow * E), Space Complexity:-
from collections import defaultdict
class Graph:
def __init__(self, graph):
self.graph = graph # residual graph
self. ROW = len(graph)
# self.COL = len(gr[0])
'''Returns true if there is a path from source 's' to sink 't' in
residual graph. Also fills parent[] to store the path '''
def BFS(self, s, t, parent):
# Mark all the vertices as not visited
visited = [False]*(self.ROW)
# Create a queue for BFS
queue = []
# Mark the source node as visited and enqueue it
queue.append(s)
visited[s] = True
# Standard BFS Loop
while queue:
# Dequeue a vertex from queue and print it
u = queue.pop(0)
# Get all adjacent vertices of the dequeued vertex u
# If a adjacent has not been visited, then mark it visited and enqueue it
for ind, val in enumerate(self.graph[u]):
if visited[ind] == False and val > 0:
# If we find a connection to the sink node, then there is no point in BFS anymore
# We just have to set its parent and can return true
queue.append(ind)
visited[ind] = True
parent[ind] = u
if ind == t:
return True
# We didn't reach sink in BFS starting from source, so return false
return False
# Returns the maximum flow from s to t in the given graph
def FordFulkerson(self, source, sink):
# This array is filled by BFS and to store path
parent = [-1]*(self.ROW)
max_flow = 0 # There is no flow initially
# Augment the flow while there is path from source to sink
while self.BFS(source, sink, parent) :
# Find minimum residual capacity of the edges along the path filled by BFS.
# Or we can say find the maximum flow through the path found.
path_flow = float("Inf")
s = sink
while(s != source):
path_flow = min (path_flow, self.graph[parent[s]][s])
s = parent[s]
# Add path flow to overall flow
max_flow += path_flow
# update residual capacities of the edges and reverse edges along the path
v = sink
while(v != source):
u = parent[v]
self.graph[u][v] -= path_flow
self.graph[v][u] += path_flow
v = parent[v]
return max_flow
Backtracking Algorithm
Looks through all solutions and the ones that fail to satisfy the problem's constraints will be removed - leaving behind the ideal solution.
Backtracking is better than naive approach because it immediately eliminates a option when it doesn't work while naive generates all options and then checks for validity.
There are 3 types:
Backtracking is better than naive approach because it immediately eliminates a option when it doesn't work while naive generates all options and then checks for validity.
There are 3 types:
- Decision Problem - search for a feasible solution
- Optimization Problem - search for the best solution
- Enumeration Problem - find all feasible solutions
N-Queens
The N Queen is the problem of placing N chess queens on an N×N chessboard so that no two queens attack each other.
# Output will be a binary matrix of NxN where 1s represent a queen and 0s represent empty square
# Starting from the leftmost column, place a queen in a column => check for clashes (w/ already placed queens). In the current column
# If no clash, add it to solution, else if no such row due => we backtrack and return false.
Time Complexity: O(n!), Space Complexity: O(n)
global N
N = 4
def printSolution(board):
for i in range(N):
for j in range(N):
print (board[i][j],end=' ')
print()
# only called after `col` queens are placed correctly from 0 to col-1 => so we only need to check the left side for all attacking queens
def isSafe(board, row, col):
# Check left side of given row
for i in range(col):
if board[row][i] == 1:
return False
# Check upper diagonal on left side
for i, j in zip(range(row, -1, -1), range(col, -1, -1)):
if board[i][j] == 1:
return False
# Check lower diagonal on left side
for i, j in zip(range(row, N, 1), range(col, -1, -1)):
if board[i][j] == 1:
return False
return True
def solveNQUtil(board, col):
# base case: If all queens are placed then return true
if col >= N:
return True
# Try placing this queen in each row one by one
for i in range(N):
if isSafe(board, i, col):
board[i][col] = 1
# Call recursion to place the next queen
if solveNQUtil(board, col + 1) == True:
return True
# If placing queen in board[i][col] != True, then remove the queen we currently placed
board[i][col] = 0
return False
# Main Function
def solveNQ():
board = [ [0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0]
]
if solveNQUtil(board, 0) == False:
print ("Solution does not exist")
return False
printSolution(board)
return True
The N Queen is the problem of placing N chess queens on an N×N chessboard so that no two queens attack each other.
# Output will be a binary matrix of NxN where 1s represent a queen and 0s represent empty square
# Starting from the leftmost column, place a queen in a column => check for clashes (w/ already placed queens). In the current column
# If no clash, add it to solution, else if no such row due => we backtrack and return false.
Time Complexity: O(n!), Space Complexity: O(n)
global N
N = 4
def printSolution(board):
for i in range(N):
for j in range(N):
print (board[i][j],end=' ')
print()
# only called after `col` queens are placed correctly from 0 to col-1 => so we only need to check the left side for all attacking queens
def isSafe(board, row, col):
# Check left side of given row
for i in range(col):
if board[row][i] == 1:
return False
# Check upper diagonal on left side
for i, j in zip(range(row, -1, -1), range(col, -1, -1)):
if board[i][j] == 1:
return False
# Check lower diagonal on left side
for i, j in zip(range(row, N, 1), range(col, -1, -1)):
if board[i][j] == 1:
return False
return True
def solveNQUtil(board, col):
# base case: If all queens are placed then return true
if col >= N:
return True
# Try placing this queen in each row one by one
for i in range(N):
if isSafe(board, i, col):
board[i][col] = 1
# Call recursion to place the next queen
if solveNQUtil(board, col + 1) == True:
return True
# If placing queen in board[i][col] != True, then remove the queen we currently placed
board[i][col] = 0
return False
# Main Function
def solveNQ():
board = [ [0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0]
]
if solveNQUtil(board, 0) == False:
print ("Solution does not exist")
return False
printSolution(board)
return True
M - Coloring Problem
Given an undirected graph and a number m, determine if the graph can be coloured with at most m colours such that no two adjacent vertices of the graph are colored with the same color.
Approach: Assign colors one by one to different vertices, starting from the vertex 0. Before assigning a color, check for safety by considering already assigned colors to the adjacent vertices i.e check if the adjacent vertices have the same color or not. If there is any color assignment that does not violate the conditions, mark the color assignment as part of the solution. If no assignment of color is possible then backtrack and return false.
Time Complexity: O(m^V), Space Complexity: O(V)
# The input graph will be provided through an adjacency matrix and the output will be a color array where color[i] is the color value of the ith vertex
class Graph():
def __init__(self, vertices):
self.V = vertices
self.graph = [[0 for column in range(vertices)] for row in range(vertices)]
# Checks if current color assignment is safe for vertex v
def isSafe(self, v, colour, c):
for i in range(self.V):
if self.graph[v][i] == 1 and colour[i] == c:
return False
return True
# Recursive function to solve m-coloring problem
def graphColourUtil(self, m, colour, v):
# base case: If all vertices have a color assigned correctly
if v == self.V:
return True
# For the current vertex, try assigning 1 out of the m-colors
for c in range(1, m + 1):
if self.isSafe(v, colour, c) == True:
colour[v] = c
# Call recursion to see if a color can be assigned successfully to the next vertex with the current color chosen
if self.graphColourUtil(m, colour, v + 1) == True:
return True
# Else remove the color and try another color for the vertex
colour[v] = 0
def graphColouring(self, m):
colour = [0] * self.V
if self.graphColourUtil(m, colour, 0) == None:
return False
# Print the solution
print ("Solution exist and Following are the assigned colours:")
for c in colour:
print (c,end=' ')
return True
Given an undirected graph and a number m, determine if the graph can be coloured with at most m colours such that no two adjacent vertices of the graph are colored with the same color.
Approach: Assign colors one by one to different vertices, starting from the vertex 0. Before assigning a color, check for safety by considering already assigned colors to the adjacent vertices i.e check if the adjacent vertices have the same color or not. If there is any color assignment that does not violate the conditions, mark the color assignment as part of the solution. If no assignment of color is possible then backtrack and return false.
Time Complexity: O(m^V), Space Complexity: O(V)
# The input graph will be provided through an adjacency matrix and the output will be a color array where color[i] is the color value of the ith vertex
class Graph():
def __init__(self, vertices):
self.V = vertices
self.graph = [[0 for column in range(vertices)] for row in range(vertices)]
# Checks if current color assignment is safe for vertex v
def isSafe(self, v, colour, c):
for i in range(self.V):
if self.graph[v][i] == 1 and colour[i] == c:
return False
return True
# Recursive function to solve m-coloring problem
def graphColourUtil(self, m, colour, v):
# base case: If all vertices have a color assigned correctly
if v == self.V:
return True
# For the current vertex, try assigning 1 out of the m-colors
for c in range(1, m + 1):
if self.isSafe(v, colour, c) == True:
colour[v] = c
# Call recursion to see if a color can be assigned successfully to the next vertex with the current color chosen
if self.graphColourUtil(m, colour, v + 1) == True:
return True
# Else remove the color and try another color for the vertex
colour[v] = 0
def graphColouring(self, m):
colour = [0] * self.V
if self.graphColourUtil(m, colour, 0) == None:
return False
# Print the solution
print ("Solution exist and Following are the assigned colours:")
for c in colour:
print (c,end=' ')
return True
Generate all Binary Strings
Time Complexity: O(2^n), Space Complexity: O(n)
def printTheArray(arr, n):
for i in range(0, n):
print(arr[i], end = " ")
print()
def generateAllBinaryStrings(n, arr, i):
# base case: if we reached length n, then we traversed all binary str combination, print the final result
if i == n:
printTheArray(arr, n)
return
# First try assigning "0" at ith position and get all other permutations for remaining positions
arr[i] = 0
generateAllBinaryStrings(n, arr, i + 1)
# Now try assign "1" at ith position and get all other permutations for remaining positions
arr[i] = 1
generateAllBinaryStrings(n, arr, i + 1)
# Driver Code
arr = [None] * n
generateAllBinaryStrings(4, arr, 0)
Time Complexity: O(2^n), Space Complexity: O(n)
def printTheArray(arr, n):
for i in range(0, n):
print(arr[i], end = " ")
print()
def generateAllBinaryStrings(n, arr, i):
# base case: if we reached length n, then we traversed all binary str combination, print the final result
if i == n:
printTheArray(arr, n)
return
# First try assigning "0" at ith position and get all other permutations for remaining positions
arr[i] = 0
generateAllBinaryStrings(n, arr, i + 1)
# Now try assign "1" at ith position and get all other permutations for remaining positions
arr[i] = 1
generateAllBinaryStrings(n, arr, i + 1)
# Driver Code
arr = [None] * n
generateAllBinaryStrings(4, arr, 0)
Detect Hamiltonian Cycle
Given a graph, check if it contains a *Hamiltonian Cycle
*Hamiltonian Cycle: Given an undirected graph, if there's a path that visits every vertex (not like MST which is more of a tree and this a path) exactly once and the first and last vertex can be connected => it contains a Hamiltonian Cycle
Approach: Create an empty path array and add vertex 0 and others to it. Before adding a vertex
=> check if it is adjacent to the previously added vertex and not already added
- If yes => add the vertex to solution.
If we do not find a vertex then we return false
class Graph():
def __init__(self, vertices):
self.graph = [[0 for column in range(vertices)] for row in range(vertices)]
self.V = vertices
# Check if this vertex is an adjacent vertex of the previously added vertex and is not included in the path earlier
def isSafe(self, v, pos, path):
# Check if current vertex and last vertex in path are adjacent
if self.graph[ path[pos-1] ][v] == 0:
return False
# Check if current vertex is not already in path
for vertex in path:
if vertex == v:
return False
return True
def hamCycleUtil(self, path, pos):
# base case: if all vertices are included in the path
if pos == self.V:
# Last & first vertex must be adjacent
if self.graph[ path[pos-1] ][ path[0] ] == 1:
return True
else:
return False
# Try different vertices as a next candidate in Hamiltonian Cycle. (Don't try 0 since it is our starting point
for v in range(1,self.V):
if self.isSafe(v, pos, path) == True:
path[pos] = v
if self.hamCycleUtil(path, pos+1) == True:
return True
# Remove current vertex if it doesn't lead to a solution
path[pos] = -1
return False
def hamCycle(self):
path = [-1] * self.V
# Starting point = vertex0 => If there is a Hamiltonian Cycle, then the path can be started from any point
path[0] = 0
if self.hamCycleUtil(path,1) == False:
print ("Solution does not exist\n")
return False
self.printSolution(path)
return True
def printSolution(self, path):
print ("Solution Exists: Following is one Hamiltonian Cycle")
for vertex in path:
print (vertex, end = " ")
print (path[0], "\n")
Given a graph, check if it contains a *Hamiltonian Cycle
*Hamiltonian Cycle: Given an undirected graph, if there's a path that visits every vertex (not like MST which is more of a tree and this a path) exactly once and the first and last vertex can be connected => it contains a Hamiltonian Cycle
Approach: Create an empty path array and add vertex 0 and others to it. Before adding a vertex
=> check if it is adjacent to the previously added vertex and not already added
- If yes => add the vertex to solution.
If we do not find a vertex then we return false
class Graph():
def __init__(self, vertices):
self.graph = [[0 for column in range(vertices)] for row in range(vertices)]
self.V = vertices
# Check if this vertex is an adjacent vertex of the previously added vertex and is not included in the path earlier
def isSafe(self, v, pos, path):
# Check if current vertex and last vertex in path are adjacent
if self.graph[ path[pos-1] ][v] == 0:
return False
# Check if current vertex is not already in path
for vertex in path:
if vertex == v:
return False
return True
def hamCycleUtil(self, path, pos):
# base case: if all vertices are included in the path
if pos == self.V:
# Last & first vertex must be adjacent
if self.graph[ path[pos-1] ][ path[0] ] == 1:
return True
else:
return False
# Try different vertices as a next candidate in Hamiltonian Cycle. (Don't try 0 since it is our starting point
for v in range(1,self.V):
if self.isSafe(v, pos, path) == True:
path[pos] = v
if self.hamCycleUtil(path, pos+1) == True:
return True
# Remove current vertex if it doesn't lead to a solution
path[pos] = -1
return False
def hamCycle(self):
path = [-1] * self.V
# Starting point = vertex0 => If there is a Hamiltonian Cycle, then the path can be started from any point
path[0] = 0
if self.hamCycleUtil(path,1) == False:
print ("Solution does not exist\n")
return False
self.printSolution(path)
return True
def printSolution(self, path):
print ("Solution Exists: Following is one Hamiltonian Cycle")
for vertex in path:
print (vertex, end = " ")
print (path[0], "\n")
Maze Problem
A maze is an NxN binary matrix. Source block is maze[0][0] and Destination block is maze[N-1][N-1]. You can only move right(forward) and down. Each element value of 0 in the maze is a dead end and 1 means it can be used in the solution path.
A maze is an NxN binary matrix. Source block is maze[0][0] and Destination block is maze[N-1][N-1]. You can only move right(forward) and down. Each element value of 0 in the maze is a dead end and 1 means it can be used in the solution path.
|
Sample Input
{1, 0, 0, 0} {1, 1, 0, 1} {0, 1, 0, 0} {1, 1, 1, 1} |
Sample Output
{1, 0, 0, 0} {1, 1, 0, 0} {0, 1, 0, 0} {0, 1, 1, 1} |
Time Complexity: O(2^(n^2)), Space Complexity: O(n^2)
# Maze size
n = 4
# Checks if the new (x,y) is a valid move
def isValid(n, maze, x, y, res):
if x >= 0 and y >= 0 and x < n and y < n and maze[x][y] == 1 and res[x][y] == 0:
return True
return False
def RatMaze(n, maze, move_x, move_y, x, y, res):
# base case: if (x, y) is destination block return True
if x == n-1 and y == n-1:
return True
for i in range(4): # len of move_x and move_y
# Generate new value of x and y
x_new = x + move_x[i]
y_new = y + move_y[i]
# If the new move is a valid move => mark it as part of the solution
if isValid(n, maze, x_new, y_new, res):
res[x_new][y_new] = 1
# If the current move can help reach the solution => return True
if RatMaze(n, maze, move_x, move_y, x_new, y_new, res):
return True
# Else erase the move and continue looking for other moves
res[x_new][y_new] = 0
return False
def solveMaze(maze):
# Initialize the output matrix with all 0s
res = [[0 for i in range(n)] for i in range(n)]
res[0][0] = 1
# x and y move matrices for each direction
move_x = [-1, 1, 0, 0]
move_y = [0, 0, -1, 1]
if RatMaze(n, maze, move_x, move_y, 0, 0, res):
for i in range(n):
for j in range(n):
print(res[i][j], end=' ')
print()
else:
print('Solution does not exist')
# Driver code
maze = [[1, 0, 0, 0],
[1, 1, 0, 1],
[0, 1, 0, 0],
[1, 1, 1, 1]]
solveMaze(maze)
# Maze size
n = 4
# Checks if the new (x,y) is a valid move
def isValid(n, maze, x, y, res):
if x >= 0 and y >= 0 and x < n and y < n and maze[x][y] == 1 and res[x][y] == 0:
return True
return False
def RatMaze(n, maze, move_x, move_y, x, y, res):
# base case: if (x, y) is destination block return True
if x == n-1 and y == n-1:
return True
for i in range(4): # len of move_x and move_y
# Generate new value of x and y
x_new = x + move_x[i]
y_new = y + move_y[i]
# If the new move is a valid move => mark it as part of the solution
if isValid(n, maze, x_new, y_new, res):
res[x_new][y_new] = 1
# If the current move can help reach the solution => return True
if RatMaze(n, maze, move_x, move_y, x_new, y_new, res):
return True
# Else erase the move and continue looking for other moves
res[x_new][y_new] = 0
return False
def solveMaze(maze):
# Initialize the output matrix with all 0s
res = [[0 for i in range(n)] for i in range(n)]
res[0][0] = 1
# x and y move matrices for each direction
move_x = [-1, 1, 0, 0]
move_y = [0, 0, -1, 1]
if RatMaze(n, maze, move_x, move_y, 0, 0, res):
for i in range(n):
for j in range(n):
print(res[i][j], end=' ')
print()
else:
print('Solution does not exist')
# Driver code
maze = [[1, 0, 0, 0],
[1, 1, 0, 1],
[0, 1, 0, 0],
[1, 1, 1, 1]]
solveMaze(maze)
Knight's Tour
Given a NxN board w/ Knight placed on board[0][0], the Knight must visit each square exactly once.
Example:
Input :
N = 8
Output:
0 59 38 33 30 17 8 63
37 34 31 60 9 62 29 16
58 1 36 39 32 27 18 7
35 48 41 26 61 10 15 28
42 57 2 49 40 23 6 19
47 50 45 54 25 20 11 14
56 43 52 3 22 13 24 5
51 46 55 44 53 4 21 12
Time Complexity: O(8^(n^2)), Space Complexity: O(n^2)
# Chessboard Size
n = 8
# Checks if (x, y) are valid indexes for N*N chessboard
def isSafe(x, y, board):
if(x >= 0 and y >= 0 and x < n and y < n and board[x][y] == -1):
return True
return False
def printSolution(n, board):
for i in range(n):
for j in range(n):
print(board[i][j], end=' ')
print()
def solveKTUtil(n, board, curr_x, curr_y, move_x, move_y, pos):
# base case: If we visited all the squares on the chess board
if(pos == n**2):
return True
# Try all next moves from the current coordinate x, y
for i in range(8):
new_x = curr_x + move_x[i]
new_y = curr_y + move_y[i]
if(isSafe(new_x, new_y, board)):
board[new_x][new_y] = pos
# If the new move leads to a solution => return True
if(solveKTUtil(n, board, new_x, new_y, move_x, move_y, pos+1)):
return True
# Else backtrack and remove the new move that we just made (-1 is default value of an untouched square)
board[new_x][new_y] = -1
return False
def solveKT(n):
# Initialization of Board matrix
board = [[-1 for i in range(n)]for i in range(n)]
# move_x and move_y define next move of Knight - move_x/y is for next value of x/y coordinate
move_x = [2, 1, -1, -2, -2, -1, 1, 2]
move_y = [1, 2, 2, 1, -1, -2, -2, -1]
# Knight is initially at the first block
board[0][0] = 0
# Step counter for knight's position
pos = 1
if(not solveKTUtil(n, board, 0, 0, move_x, move_y, pos)):
print("Solution does not exist")
else:
printSolution(n, board)
Given a NxN board w/ Knight placed on board[0][0], the Knight must visit each square exactly once.
Example:
Input :
N = 8
Output:
0 59 38 33 30 17 8 63
37 34 31 60 9 62 29 16
58 1 36 39 32 27 18 7
35 48 41 26 61 10 15 28
42 57 2 49 40 23 6 19
47 50 45 54 25 20 11 14
56 43 52 3 22 13 24 5
51 46 55 44 53 4 21 12
Time Complexity: O(8^(n^2)), Space Complexity: O(n^2)
# Chessboard Size
n = 8
# Checks if (x, y) are valid indexes for N*N chessboard
def isSafe(x, y, board):
if(x >= 0 and y >= 0 and x < n and y < n and board[x][y] == -1):
return True
return False
def printSolution(n, board):
for i in range(n):
for j in range(n):
print(board[i][j], end=' ')
print()
def solveKTUtil(n, board, curr_x, curr_y, move_x, move_y, pos):
# base case: If we visited all the squares on the chess board
if(pos == n**2):
return True
# Try all next moves from the current coordinate x, y
for i in range(8):
new_x = curr_x + move_x[i]
new_y = curr_y + move_y[i]
if(isSafe(new_x, new_y, board)):
board[new_x][new_y] = pos
# If the new move leads to a solution => return True
if(solveKTUtil(n, board, new_x, new_y, move_x, move_y, pos+1)):
return True
# Else backtrack and remove the new move that we just made (-1 is default value of an untouched square)
board[new_x][new_y] = -1
return False
def solveKT(n):
# Initialization of Board matrix
board = [[-1 for i in range(n)]for i in range(n)]
# move_x and move_y define next move of Knight - move_x/y is for next value of x/y coordinate
move_x = [2, 1, -1, -2, -2, -1, 1, 2]
move_y = [1, 2, 2, 1, -1, -2, -2, -1]
# Knight is initially at the first block
board[0][0] = 0
# Step counter for knight's position
pos = 1
if(not solveKTUtil(n, board, 0, 0, move_x, move_y, pos)):
print("Solution does not exist")
else:
printSolution(n, board)
Sudoku
Given a partially filled 9×9 2D array ‘grid[9][9]’ => complete the sudoku. Below is an example
Given a partially filled 9×9 2D array ‘grid[9][9]’ => complete the sudoku. Below is an example
|
Input:
grid = { {3, 0, 6, 5, 0, 8, 4, 0, 0}, {5, 2, 0, 0, 0, 0, 0, 0, 0}, {0, 8, 7, 0, 0, 0, 0, 3, 1}, {0, 0, 3, 0, 1, 0, 0, 8, 0}, {9, 0, 0, 8, 6, 3, 0, 0, 5}, {0, 5, 0, 0, 9, 0, 6, 0, 0}, {1, 3, 0, 0, 0, 0, 2, 5, 0}, {0, 0, 0, 0, 0, 0, 0, 7, 4}, {0, 0, 5, 2, 0, 6, 3, 0, 0} } |
Output:
3 1 6 5 7 8 4 9 2 5 2 9 1 3 4 7 6 8 4 8 7 6 2 9 5 3 1 2 6 3 4 1 5 9 8 7 9 7 4 8 6 3 1 2 5 8 5 1 7 9 2 6 4 3 1 3 8 9 4 7 2 5 6 6 9 2 3 5 1 8 7 4 7 4 5 2 8 6 3 1 9 |
One by one assigning numbers to empty cells.
Check whether it is safe to assign => Check that the same number is not present in the current row, current column and current 3X3 subgrid. Check whether this assignment leads to a solution or not.
- If not, then try the next number for the current empty cell. And if none exists, return false and print no solution exists.
Time Complexity: O(9^(n^2)), Space Complexity: O(n^2)
def print_grid(arr):
for i in range(9):
for j in range(9):
print arr[i][j],
print ('\n')
# Initially, l = [0, 0], but eventually l = [some_row, some_col], find the next empty box on sudoku board (empty boxes filled with 0)
def find_empty_location(arr, l):
for row in range(9):
for col in range(9):
if(arr[row][col]== 0):
l[0]= row
l[1]= col
return True
return False
# Given a row, checks if the num is already present in the row of the sudoku arr
def used_in_row(arr, row, num):
for i in range(9):
if(arr[row][i] == num):
return True
return False
# Given a col, checks if the num is already present in the col of the sudoku arr
def used_in_col(arr, col, num):
for i in range(9):
if(arr[i][col] == num):
return True
return False
# Given a row&col, checks if the num is already present in the box of the sudoku arr
def used_in_box(arr, row, col, num):
for i in range(3):
for j in range(3):
if(arr[i + row][j + col] == num):
return True
return False
# Given a row&col checks if the num can be placed in the box correctly
def check_location_is_safe(arr, row, col, num):
return not used_in_row(arr, row, num) and not used_in_col(arr, col, num) and not used_in_box(arr, row - row % 3, col - col % 3, num)
def solve_sudoku(arr):
# l keeps track of which row and col we're working on
l =[0, 0]
# base case: all boxes on sudoku arr are filled
if(not find_empty_location(arr, l)):
return True
# Assigns the next empty row & col
row = l[0]
col = l[1]
# Digits from 1 to 9
for num in range(1, 10):
# check if num can be placed correctly in the current empty (row, col)
if(check_location_is_safe(arr, row, col, num)):
# then assign it
arr[row][col]= num
# if the current assignment leads to the solution => return True
if(solve_sudoku(arr)):
return True
# else backtrack, and remove the current assignment
arr[row][col] = 0
return False
# Driver code
# Initialize and set sudoku array
grid =[[0 for x in range(9)]for y in range(9)]
grid =[[3, 0, 6, 5, 0, 8, 4, 0, 0],
[5, 2, 0, 0, 0, 0, 0, 0, 0],
[0, 8, 7, 0, 0, 0, 0, 3, 1],
[0, 0, 3, 0, 1, 0, 0, 8, 0],
[9, 0, 0, 8, 6, 3, 0, 0, 5],
[0, 5, 0, 0, 9, 0, 6, 0, 0],
[1, 3, 0, 0, 0, 0, 2, 5, 0],
[0, 0, 0, 0, 0, 0, 0, 7, 4],
[0, 0, 5, 2, 0, 6, 3, 0, 0]]
if(solve_sudoku(grid)):
print_grid(grid)
else:
print "No solution exists"
Check whether it is safe to assign => Check that the same number is not present in the current row, current column and current 3X3 subgrid. Check whether this assignment leads to a solution or not.
- If not, then try the next number for the current empty cell. And if none exists, return false and print no solution exists.
Time Complexity: O(9^(n^2)), Space Complexity: O(n^2)
def print_grid(arr):
for i in range(9):
for j in range(9):
print arr[i][j],
print ('\n')
# Initially, l = [0, 0], but eventually l = [some_row, some_col], find the next empty box on sudoku board (empty boxes filled with 0)
def find_empty_location(arr, l):
for row in range(9):
for col in range(9):
if(arr[row][col]== 0):
l[0]= row
l[1]= col
return True
return False
# Given a row, checks if the num is already present in the row of the sudoku arr
def used_in_row(arr, row, num):
for i in range(9):
if(arr[row][i] == num):
return True
return False
# Given a col, checks if the num is already present in the col of the sudoku arr
def used_in_col(arr, col, num):
for i in range(9):
if(arr[i][col] == num):
return True
return False
# Given a row&col, checks if the num is already present in the box of the sudoku arr
def used_in_box(arr, row, col, num):
for i in range(3):
for j in range(3):
if(arr[i + row][j + col] == num):
return True
return False
# Given a row&col checks if the num can be placed in the box correctly
def check_location_is_safe(arr, row, col, num):
return not used_in_row(arr, row, num) and not used_in_col(arr, col, num) and not used_in_box(arr, row - row % 3, col - col % 3, num)
def solve_sudoku(arr):
# l keeps track of which row and col we're working on
l =[0, 0]
# base case: all boxes on sudoku arr are filled
if(not find_empty_location(arr, l)):
return True
# Assigns the next empty row & col
row = l[0]
col = l[1]
# Digits from 1 to 9
for num in range(1, 10):
# check if num can be placed correctly in the current empty (row, col)
if(check_location_is_safe(arr, row, col, num)):
# then assign it
arr[row][col]= num
# if the current assignment leads to the solution => return True
if(solve_sudoku(arr)):
return True
# else backtrack, and remove the current assignment
arr[row][col] = 0
return False
# Driver code
# Initialize and set sudoku array
grid =[[0 for x in range(9)]for y in range(9)]
grid =[[3, 0, 6, 5, 0, 8, 4, 0, 0],
[5, 2, 0, 0, 0, 0, 0, 0, 0],
[0, 8, 7, 0, 0, 0, 0, 3, 1],
[0, 0, 3, 0, 1, 0, 0, 8, 0],
[9, 0, 0, 8, 6, 3, 0, 0, 5],
[0, 5, 0, 0, 9, 0, 6, 0, 0],
[1, 3, 0, 0, 0, 0, 2, 5, 0],
[0, 0, 0, 0, 0, 0, 0, 7, 4],
[0, 0, 5, 2, 0, 6, 3, 0, 0]]
if(solve_sudoku(grid)):
print_grid(grid)
else:
print "No solution exists"